Svemirska utrka
Lagrangeove točke su nova bojna polja u svemiru
Tko kontrolira Lagrangeove točke u svemiru, ima veliku prednost u istraživanju svemira, komunikacijama i nadzoru.
Američki kongresnici smatraju da će se uskoro voditi velika bitka za osvajanje takozvanih Lagrangeovih točki u svemiru, između najvećih svemirskih nacija, posebice između SAD-a i Kine te smatraju da onaj tko kontrolira Lagrangeove točke, ima veliku prednost u istraživanju svemira, komunikacijama i nadzoru.
Lagrangeove točke su položaji u prostoru gdje gravitacijske sile sustava dvaju tijela poput Sunca i Zemlje stvaraju pojačana područja privlačenja i odbijanja. Svemirske letjelice ih mogu koristiti kao "parkirališta" u svemiru kako bi ostale u fiksnom položaju uz minimalnu potrošnju goriva.
Postoji pet posebnih točaka u kojima mala masa može kružiti u konstantnom uzorku s dvije veće mase. Lagrangeove točke su položaji u kojima je gravitacijska sila dviju velikih masa točno jednaka centripetalnoj sili potrebnoj da se mali objekt kreće s njima. Ovaj matematički problem, poznat kao "Opći problem tri tijela" razmatrao je talijansko-francuski matematičar Joseph-Louis Lagrange u svom nagrađenom radu 'Essai sur le Problème des Trois Corps' , 1772. godine, a više o njima možete saznati u ovom videu.
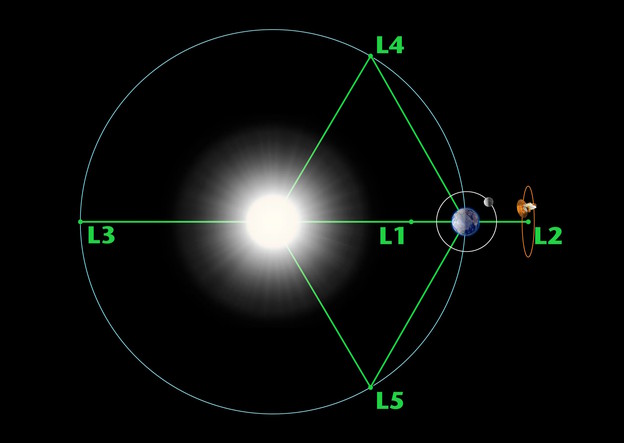
Od pet Lagrangeovih točaka tri su nestabilne, a dvije stabilne. Nestabilne Lagrangeove točke, označene s L1, L2 i L3, leže duž linije koja povezuje dvije velike mase. Stabilne Lagrangeove točke, označene s L4 i L5, tvore vrh dva jednakostranična trokuta koji imaju velike mase na svojim vrhovima. L4 vodi zemljinu orbitu, a L5 slijedi.
Točka L1 sustava Zemlja-Sunce omogućuje neprekinuti pogled na Sunce i trenutno je dom satelita Solar and Heliospheric Observatory Satellite SOHO.
Točka L2 sustava Zemlja-Sunce bila je dom svemirske letjelice WMAP, dom Europskog svemirskog opservatorija Planck i svemirskog teleskopa James Webb.
L2 je idealan za astronomiju jer je svemirska letjelica dovoljno blizu da lako komunicira sa Zemljom, može držati Sunce, Zemlju i Mjesec iza letjelice za dobivanje solarne energije i teleskopima pruža jasan pogled na duboki svemir. Točke L1 i L2 nestabilne su na vremenskoj skali od približno 23 dana, što zahtijeva da sateliti koji kruže oko ovih pozicija prolaze redovite korekcije kursa i položaja.
Kina je već poslala relejni satelit Queqiao na L2 u sustavu Zemlja-Mjesec za komunikaciju s lunarnom sondom Chang'e 4, prvom koja je sletjela na suprotnu (tamnu) stranu Mjeseca. SAD također cilja na sustav Zemlja-Mjesec L2, s misijama poput lunarne ispostave Gateway planirane za kasne 2020-e.
Američko-kinesko gospodarsko i tehnološko suparništvo bilo je predmet nedavnog izvješća dvostranačkog odbora Zastupničkog doma američkog Kongresa u kojem se istaknuo jedan prijedlog koji se odnosi na svemir. Prema tom prijedlogu Kongres bi trebao financirati NASA-ine programe i programe Ministarstva obrane koji su ključni za suprotstavljanje ambicijama Kineske komunističke partije (KPK) u svemiru, uključujući osiguravanje da Sjedinjene Države budu prva zemlja koja će trajno stacionirati letjelice i satelite na svim Lagrangeovim točkama.
"KPK dobro razumije potrebu za operacijama baziranim u svemiru i razvija zastrašujuće svemirske sposobnosti za izazov američkoj dominaciji u tom području. NASA i nadležni Odjel za Financiranje obrane ključni su za osiguranje zapovijedanja i kontrole u svemirskoj domeni, kako bi uspostaviti dominaciju u multilateralnom upravljanju svemirom i potaknuli znanstvena otkrića i američke inovacije", navodi se u dokumentu koji je izdao američki Kongres.
Kako se čini, Lagrangeove točke bi mogle postati novo bojno polje u svemirskoj utrci, možda čak i prije nego što se hladni svemirski rat počne odvijati na Mjesecu i Marsu, kao što to ukazuje alternativna prošlost u odličnoj TV seriji For All Mankind koju vam toplo preporučamo.

Učitavam komentare ...